domingo, 25 de septiembre de 2011

~Movimiento Parabolico~

Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.
Puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical.





Tir parabòlic.png




Ecuaciones del Movimiento Parabolico


Hay dos ecuaciones que rigen el movimiento parabólico:
  1. \mathbf{v_0} = v_0 \, \cos{\phi} \, \mathbf{i} + v_0 \, \sin{\phi} \, \mathbf{j}
  2. \mathbf{a} = -g \, \mathbf{j}
donde:
v_0 \, es el módulo de la velocidad inicial.
\phi \, es el ángulo de la velocidad inicial sobre la horizontal.
g \, es la aceleración de la gravedad.
La velocidad inicial se compone de dos partes:
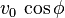v_0 \, \cos{\phi} que se denomina componente horizontal de la velocidad inicial.
En lo sucesivo v_{0x} \,
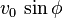v_0 \, \sin{\phi} que se denomina componente vertical de la velocidad inicial.
En lo sucesivo v_{0y} \,
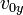
Se puede expresar la velocidad inicial de este modo:
\mathbf{v_0} = v_{0x} \, \mathbf{i} + v_{0y} \, \mathbf{j}  : [ecu. 1]
Publicado por en

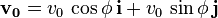
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)